| . ___ __ __ ___ . __ __ __ __ __ __ | | |__ |__) |__) |__ ' /__` /__` / \ /\ |__) |__) / \ \_/ |___ | |___ | \ | \ |___ .__/ .__/ \__/ /~~\ | |__) \__/ / \ ⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∽⋅∼⋅∽⋅∽⋅∽⋅∽⋅
We're creating a little program that takes in a soundfile, estimates the pitch and returns it as human readable notation. See previously:
specification and motivation
implementation planning
dev log 0
dev log 1
dev log 2
Last time, we reframed the problem and tackled the issue of transforming the raw sample to fundamental frequency. Then cut it with an edge detector and finally process each segment by simply taking the median frequency and converting it to notes. It looks like this:
import librosa
import matplotlib.pyplot as plt
import scipy.ndimage as sim
y, sr = librosa.load("twinkle.wav")
## Extract the fundamental frequency
f0, voiced_flag, voiced_probs = librosa.pyin(y,
sr=sr,
fmin=librosa.note_to_hz('C0'),
fmax=librosa.note_to_hz('C9'),
fill_na=None)
times = librosa.times_like(f0)
## Segment the fundamental frequency
sobelified_f0=sim.sobel(f0)
# Cut it by noticing the moments where we go
# from non null values back to zero
a = 0
note_shifts=[]
for i,v in enumerate(sobelified_f0):
if v!=0:
a=v
if a!=0 and v==0:
note_shifts.append(times[i])
a=0
## Process each segment and converts it to music notes
music_sheet = []
for i in range(len(note_shifts)-1):
median_frequency = np.median(f0[(note_shifts[i]<=times) & (times<=note_shifts[i+1])])
music_sheet.append(librosa.hz_to_note(median_frequency))
" ".join(music_sheet)
Now, we tested it on one sample so far, which is twinkle twinkle little star produced with a digital instrument. The goal of this program is to handle voice. So it is time to:
Then we'll see.
In order to create a good voice sample, I'll just use the best microphone I have around, which is my smartphone. To make sure that I sing as accurately as possible, I'll play the digitally created sample in one of my ears at the same time. Then I'll use Audacity to loop over each sung notes and use a tuner app to confirm that the notes are accurate.
Reminder, we focus on the start of Twinkle Twinkle Little Star, which goes:
C3 C3 G3 G3 A3 A3 G3 F3 F3 E3 E3 D3 D3 C3
We can accept C3 G3 A3 G3 F3 E3 D3 C3 given that the program does not know how to handle repeating notes (or held notes) yet.
So I just executed the plan above, fed it to the program, and it yielded:
B8 C9 A♯8 A♯8 C9 A♯8 A♯8 B8 F♯6 C3 C3 C3 C3 C3 C3 D♯3 G3 G3 G3 G3 G3 G3 G3 A3 A3 A3 A3 A3 A3 G♯3 G3 G3 F♯3 F3 F3 F3 F3 F3 F3 F3 F3 E3 E3 E3 E3 E3 E3 E3 E3 E3 E3 D3 D3 D3 D3 D3 C3 C3 C3 C3 D2
On the bright side, I do sing accurately enough so that both the tuner and the program agree that the C3 G3 A3 G3 F3 E3 D3 C3 melody can be read in there.
But there is also many, many more notes that I do not really want.
Looking at the fundamental frequency, we see some of the issue. There are unwanted frequencies in there, as expected. Especially in the silent start.
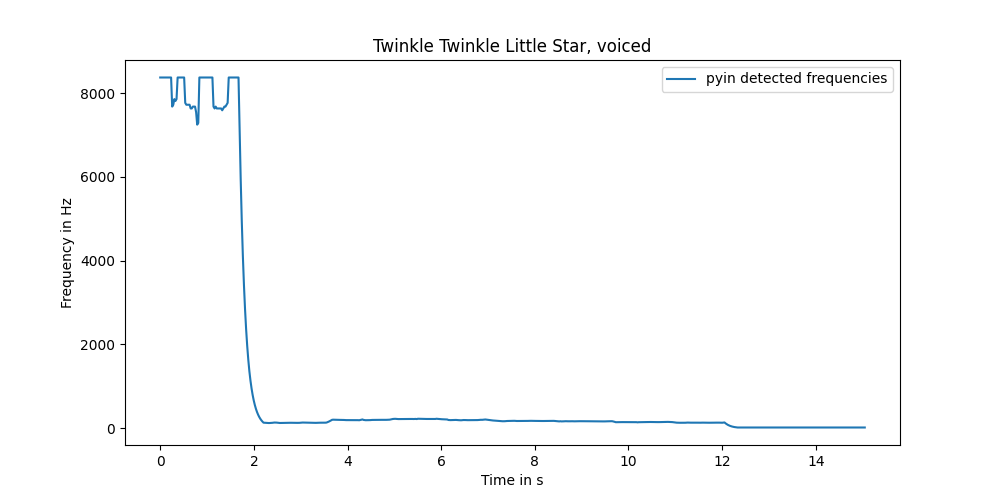
I tried librosa.effects.trim again and with the right parameters, it looks better.
y_trimmed, _ = librosa.effects.trim(y, top_db=30)
f0, voiced_flag, voiced_probs = librosa.pyin(y_trimmed,
sr=sr,
fmin=librosa.note_to_hz('C0'),
fmax=librosa.note_to_hz('C9'),
fill_na=None)
times = librosa.times_like(f0)
f,a = plt.subplots()
a.plot(times,f0,label="pyin detected frequencies")
a.legend()
a.set_xlabel("Time in s")
a.set_ylabel("Frequency in Hz")
a.set_title("Twinkle Twinkle Little Star, voiced after filtering")
f.set_size_inches(10,5)
f.savefig("twinkle_twinkle_little_star_sample_voice_pitch_filtered.png")
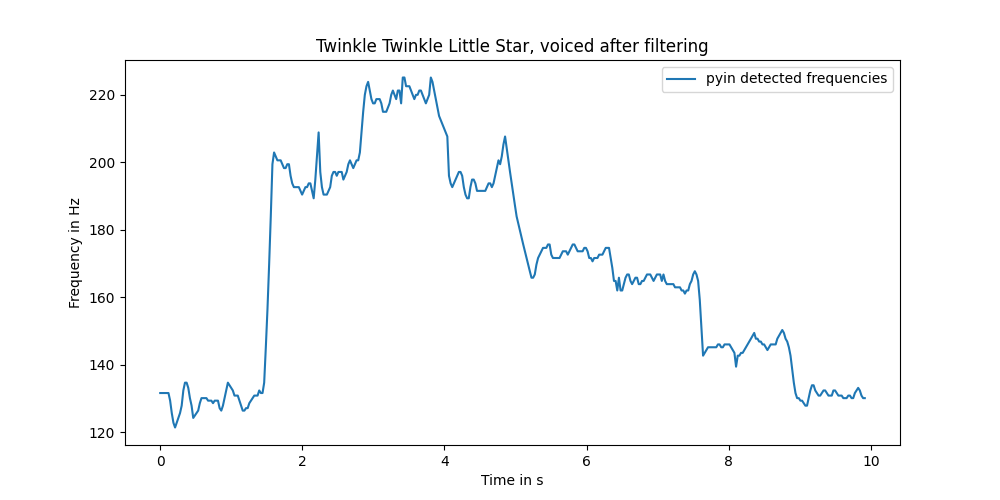
And how does the rest of the algorithm tread it afterward?
C3 C3 C3 C3 C3 C3 D♯3 G3 G3 G3 G3 G3 G3 G3 A3 A3 A3 A3 A3 A3 G♯3 G3 G3 F♯3 F3 F3 F3 F3 F3 F3 F3 F3 E3 E3 E3 E3 E3 E3 E3 E3 E3 E3 D3 D3 D3 D3 D3 C3 C3 C3 C3 C3
Better, better but not there yet. It's quite evident why when you look at it:
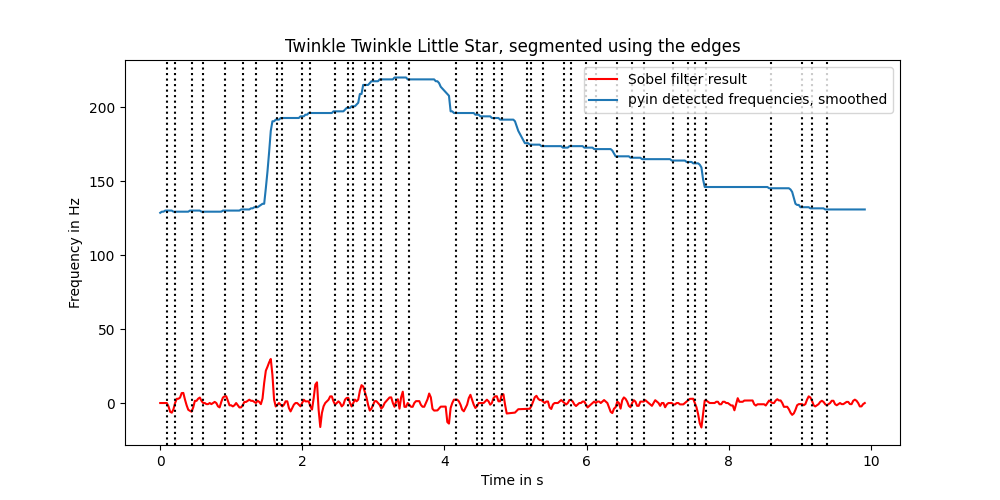
The Sobel detector, doing its job, interprets each little variation as an edge. The simplistic note cutting algorithm then goes over it and chops it into a myriad of little slices.
Alright, let's bring back one of the median filters and see if it can smooth this a little bit. And indeed, after playing a bit with the parameters, it can be. It still cuts things too fine, but it does not appear to be a problem of the Sobel filtering. Looking at the curve, it does its job.
The cutting logic is simply a bit too rough. Or we could make it so that the Sobel filtering result is smoother. We have something we have not used yet: the fact that we know that an edge can be no less than a semi-tone and that fact that I won't sing something faster than a sixteenth of a note.
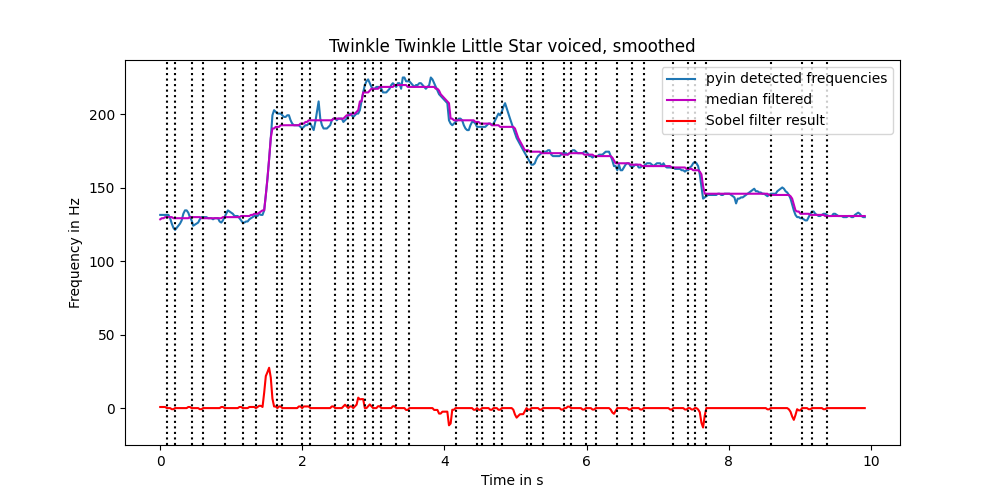
Let's see what the beat detecting abilities of librosa have to offer. In a sung samples that I'll produce, given that they are short, there probably won't be a beat switch in it. Which means that assuming constant beat is probably an acceptable assumption to make. However, can the beat be accurately discovered in short samples?
Apparently, yes. The beats array ends soon, but the tempo is accurate enough to segment the tune interestingly. We apply the frequency hypothesis as well.
tempo_in_bpm, beats = librosa.beat.beat_track(y=y_trimmed, sr=sr)
tempo_in_s = tempo_in_bpm/60.0
# creating the time index rhythmed by eighth
beat_segment = 0
eighth_of_a_note = tempo_in_s[0]/8.0
index_of_eighth = []
while beat_segment < max(times)+eighth_of_a_note:
index_of_eighth.append(np.argmin(abs(times-beat_segment)))
beat_segment += eighth_of_a_note
# frequencies
possible_notes = ["C","C#","D","D#","E","F","F#","G","G#","A","A#","B"]
possible_octaves = [0,1,2,3,4,5,6,7,8]
possible_frequencies = []
for o in possible_octaves:
for n in possible_notes:
possible_frequencies.append(librosa.note_to_hz(f"{n}{o}"))
f,a = plt.subplots()
a.plot(times,f0_median_filtered,label="pyin detected frequencies, smoothed",color='m')
a.legend()
a.set_xlabel("Time in s")
a.set_ylabel("Frequency in Hz")
a.set_title("Twinkle Twinkle Little Star, with time and frequencies assumptions")
for f_hz in possible_frequencies:
if f_hz < min(f0_median_filtered):
continue
elif max(f0_median_filtered) < f_hz:
a.axhline(f_hz,color="k",linestyle=":")
break
a.axhline(f_hz,color="k",linestyle=":")
for i in index_of_eighth:
a.axvline(times[i],color="k",linestyle=":")
f.set_size_inches(10,5)
f.savefig("twinkle_twinkle_little_star_voiced_with_assumptions.png")
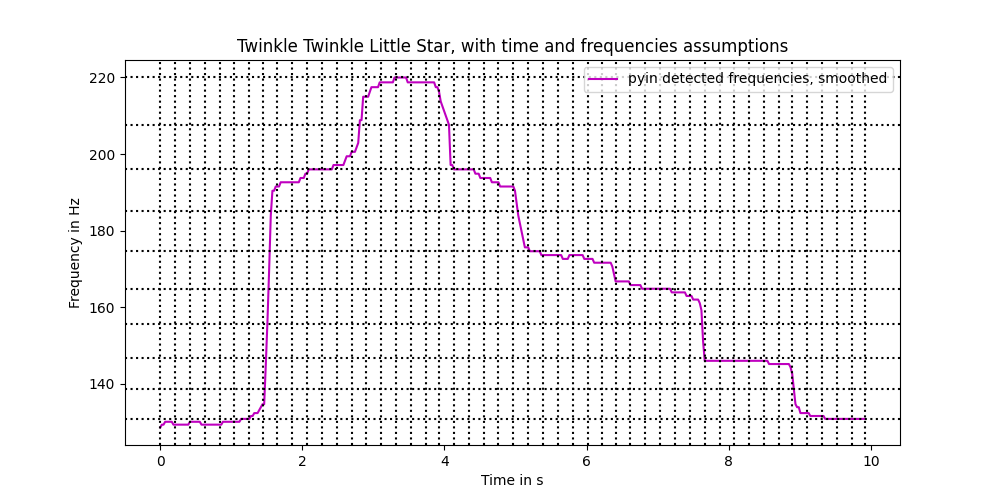
Now, it's a bit brute-forcy, but we could iterate over each of the time increments and look for the closest allowed frequency and remove duplicates.
music_sheet=[]
previous_note = ""
for i in range(len(index_of_eighth)-1):
frequency_range = f0_median_filtered[index_of_eighth[i]:index_of_eighth[i+1]]
min_allowed_note_in_hz = np.argmin(abs(possible_frequencies-min(frequency_range)))
max_allowed_note_in_hz = np.argmin(abs(possible_frequencies-max(frequency_range)))
note_range = max_allowed_note_in_hz-min_allowed_note_in_hz
arbitrary_limit = 1
if arbitrary_limit < note_range:
continue
current_note = librosa.hz_to_note(np.median(frequency_range))
if previous_note != current_note:
music_sheet.append(current_note)
previous_note = current_note
" ".join(music_sheet)
And here we are: C3 G3 A3 G3 F3 E3 D3 C3
import librosa
import matplotlib.pyplot as plt
import scipy.ndimage as sim
import scipy.signal as sig
import numpy as np
y, sr = librosa.load("twinkle_twinkle_little_star_voice_record.wav")
y_trimmed, _ = librosa.effects.trim(y, top_db=30)
## Extract the fundamental frequency
f0, voiced_flag, voiced_probs = librosa.pyin(y_trimmed,
sr=sr,
fmin=librosa.note_to_hz('C0'),
fmax=librosa.note_to_hz('C9'),
fill_na=None)
times = librosa.times_like(f0)
tempo_in_bpm, beats = librosa.beat.beat_track(y=y_trimmed, sr=sr)
tempo_in_s = tempo_in_bpm/60.0
# creating the time index rhythmed by eighth
beat_segment = 0
eighth_of_a_note = tempo_in_s[0]/8.0
index_of_eighth = []
while beat_segment < max(times)+eighth_of_a_note:
index_of_eighth.append(np.argmin(abs(times-beat_segment)))
beat_segment += eighth_of_a_note
# frequencies
filter_size = 50
f0_median_filtered = sim.median_filter(f0,size=filter_size)
possible_notes = ["C","C#","D","D#","E","F","F#","G","G#","A","A#","B"]
possible_octaves = [0,1,2,3,4,5,6,7,8]
possible_frequencies = []
for o in possible_octaves:
for n in possible_notes:
possible_frequencies.append(librosa.note_to_hz(f"{n}{o}"))
# creating the music sheet by classifying each eighth of a note
music_sheet=[]
previous_note = ""
for i in range(len(index_of_eighth)-1):
frequency_range = f0_median_filtered[index_of_eighth[i]:index_of_eighth[i+1]]
min_allowed_note_in_hz = np.argmin(abs(possible_frequencies-min(frequency_range)))
max_allowed_note_in_hz = np.argmin(abs(possible_frequencies-max(frequency_range)))
note_range = max_allowed_note_in_hz-min_allowed_note_in_hz
arbitrary_limit = 1
if arbitrary_limit < note_range:
continue
current_note = librosa.hz_to_note(np.median(frequency_range))
if previous_note != current_note:
music_sheet.append(current_note)
previous_note = current_note
" ".join(music_sheet)
Slow but works, at least on our voiced sample. However, if used on the machine produced sample, the median filtering is apparently a bit too aggressive. Removing the median filter lets bad notes slip through. Let's see if we can find a better parameter for the median filter then. The window size was set to 50 arbitrarily. Maybe we can do something based on the eighth note consistency hypothesis. A single eighth note length is apparently too small, but two seems to do the trick.
default_time_increment = np.mean(abs(times[0:-1]-times[1:])) filter_size = 2*int(np.ceil(eighth_of_a_note/default_time_increment)) f0_median_filtered = sim.median_filter(f0,size=filter_size)
And it now works for both samples! Yay! Here is the complete program:
import librosa
import matplotlib.pyplot as plt
import scipy.ndimage as sim
import scipy.signal as sig
import numpy as np
#y, sr = librosa.load("twinkle_twinkle_little_star_voice_record.wav")
y, sr = librosa.load("twinkle.wav")
y_trimmed, _ = librosa.effects.trim(y, top_db=30)
## Extract the fundamental frequency
f0, voiced_flag, voiced_probs = librosa.pyin(y_trimmed,
sr=sr,
fmin=librosa.note_to_hz('C0'),
fmax=librosa.note_to_hz('C9'),
fill_na=None)
times = librosa.times_like(f0)
tempo_in_bpm, beats = librosa.beat.beat_track(y=y_trimmed, sr=sr)
tempo_in_s = tempo_in_bpm/60.0
# creating the time index rhythmed by eighth
beat_segment = 0
eighth_of_a_note = tempo_in_s[0]/8.0
index_of_eighth = []
while beat_segment < max(times)+eighth_of_a_note:
index_of_eighth.append(np.argmin(abs(times-beat_segment)))
beat_segment += eighth_of_a_note
# frequencies
default_time_increment = np.mean(abs(times[0:-1]-times[1:]))
filter_size = 2*int(np.ceil(eighth_of_a_note/default_time_increment))
f0_median_filtered = sim.median_filter(f0,size=filter_size)
possible_notes = ["C","C#","D","D#","E","F","F#","G","G#","A","A#","B"]
possible_octaves = [0,1,2,3,4,5,6,7,8]
possible_frequencies = []
for o in possible_octaves:
for n in possible_notes:
possible_frequencies.append(librosa.note_to_hz(f"{n}{o}"))
# creating the music sheet by classifying each eighth of a note
music_sheet=[]
previous_note = ""
for i in range(len(index_of_eighth)-1):
frequency_range = f0_median_filtered[index_of_eighth[i]:index_of_eighth[i+1]]
min_allowed_note_in_hz = np.argmin(abs(possible_frequencies-min(frequency_range)))
max_allowed_note_in_hz = np.argmin(abs(possible_frequencies-max(frequency_range)))
note_range = max_allowed_note_in_hz-min_allowed_note_in_hz
arbitrary_limit = 1
if arbitrary_limit < note_range:
continue
current_note = librosa.hz_to_note(np.median(frequency_range))
if previous_note != current_note:
music_sheet.append(current_note)
previous_note = current_note
" ".join(music_sheet)
Finally, we have something that appears plausible for both ground truths. It is time for a validation test:
And the result is... ok-ish. With the generated partition, by filtering some of the cruft mentally I can retrieve the melody somewhat faster than if I was doing it by trial and error. When singing slowly, it's pretty good. When note transitions are fast, not so much. And it's also a bit cumbersome to have to transfer the recorded file from my phone to my computer.
There is definitely room for improvements. There is probably a much better way to detect those frequencies as well. Maybe by looking for correlations at the frequencies we expect and taking the best scoring ones, etc... The way used here is pretty rough. Also we might want to detect the note durations, as it would help piece the melody faster too. A visualization of the detected note heights with the fundamental frequency might actually be more informative than a simple list of strings though.
But all in all, that will be ok for now, let's make some music.
⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∼⋅∽⋅∽⋅∼⋅∽⋅∽⋅